I ended up talking a lot about certificates recently and covered quite a few topics in a good amount of detail. To demonstrate something I've touched on a few times in my recent posts I built a little tool called Chain Build so you can see how to quickly and easily identify if alternate trust paths exist for your certificates!
Why would anyone do this?
Why indeed. I built a little tool that will take a leaf certificate in PEM format and try to build as many valid certificate chains as possible. I did this to show that it is possible to build multiple chains for a given certificate and to show, at a high level, what that process looks like. I also did this because 'doing things' is how I find I learn best and I like tinkering with stuff. If you didn't read my previous posts to understand why alternate trust paths are important, you should start there.
The Impending Doom of Expiring Root CAs and Legacy Clients
The Complexities of Chain Building and CA Infrastructure
Cross-Signing and Alternate Trust Paths; How They Work
Before we dig into the tool, and calling it a 'tool' is really overstating things, we should understand that the code I wrote shouldn't be relied upon for anything and the information it provides should be relied upon even less. It was a quick and dirty script I threw together in an evening to demonstrate a point and scratch an itch, nothing more!
Getting a list of Root CAs
To get started we're going to need a few things and the first on the list is a Root Store that we can build chains down to, these will be our ultimate Trust Anchors. I decided to use the Mozilla CA Certificate Program's list of Included CA Certificates which you can download here but the format is a little raw. To save myself having to do anything with that file I'm instead going to use the list extracted and converted to PEM by Daniel Stenberg here. That gives me a list of 138 Root CA Certificates at the time of writing.
Getting a list of Intermediate CAs
This one sounds like it could be a little more tricky because the idea of having an Intermediate Store on a device isn't as familiar as having a Root Store on a device. That said though, such a concept does exist and again we turn to Mozilla to help us out. Mozilla have a feature called Intermediate Preloading that does just what it sounds like, they have a bundle of Intermediate CA Certificates that they preload into the client. The list isn't bundled into the installer but is instead fetched and built in the client at a rate of 100 Intermediate Certificates per day (at present) so if you have a clean install of Firefox for example, it could take a little while for it to fetch them all.
This list of Intermediate Certificates is taken from the CCADB, the Common CA Database, which is another project run by, you guessed it, Mozilla! If you want to extract this list of Intermediate Certificates you can use moz_crlite_query which is a tool create by, you guessed it again, Mozilla! (sometimes I wonder what the state of PKI would be without Mozilla...)
This gives us a hefty list of 2,084 Intermediate CA Certificates at present!
Why didn't I use AIA?
It's a perfectly valid question and if you aren't familiar with AIA (Authority Information Access) Fetching then you need to zip up to the top and check out the links to my previous posts where I show what the AIA field is and how AIA Fetching works. The problem with AIA Fetching is that 1) I'd have to write the code to do it and 2) it doesn't allow for the building of alternate trust paths, which is exactly the problem I'm trying to solve here. This idea that a single, valid certificate chain exists is very common and also very wrong. It's the cause of quite a few problems and something I want to demonstrate is completely false with this tool.

One Chain to rule them all
I couldn't help but hear Gandalf saying this in my head when I think about this but the typical view of certificate chains can be nicely summarised by this adapted Lord of the Rings quote:
One Chain to rule them all,
One Chain to find them,
One Chain to bring them all and in the darkness bind them.
The part that amuses me the most is the last few words of "in the darkness bind them" which I'm sure many of those who work in this field or with certificates will agree with! Back on track through and the point is that this idea that there exists "a" certificate chain or "the" certificate chain is what needs to change. What a client needs to do, and what we need to understand, is that your job is to find any chain that works and go with that, even if it's not the one that the server indicated it would prefer by including a particular intermediate. To see what that looks like, let's take a look at my hacky tool.
Chain Builder
So, how do we do this? I'm going to include the code here as the entire script is only 72 LOC but I will also link out to the GitHub repo too.
<?php
declare(strict_types = 1);
$certTypes = ['root', 'intermediate'];
foreach ($certTypes as $type)
{
${$type . "Certificates"} = array();
$certs = file_get_contents("./$type-certificates.pem");
while (strpos($certs, '-----BEGIN CERTIFICATE-----') !== false) {
$start = strpos($certs, '-----BEGIN CERTIFICATE-----');
$end = strpos($certs, '-----END CERTIFICATE-----') + 25;
$pem = substr($certs, $start, $end - $start);
${$type . "Certificates"}[] = ['pem' => $pem, 'parsed' => openssl_x509_parse($pem, false)];
$certs = substr($certs, $end);
}
}
$leaf = file_get_contents($argv[1]);
$crt = openssl_x509_parse($leaf, false);
$store[getHash($leaf)] = $crt;
if (isset($crt['extensions']['authorityKeyIdentifier'])) {
$chain = [getHash($leaf) => checkParents($crt, $certTypes, $rootCertificates, $intermediateCertificates, $store)];
prettyPrintChain($chain, $store);
}
function getHash($pem)
{
$der = base64_decode(trim(str_replace(['-----BEGIN CERTIFICATE-----', '-----END CERTIFICATE-----'], '', $pem)));
return bin2hex(hash('sha256', $der, true));
}
function checkParents($candidate, $certTypes, $rootCertificates, $intermediateCertificates, &$store)
{
$parents = [];
foreach ($certTypes as $type) {
foreach (${$type . "Certificates"} as $certificate) {
if (isset($certificate['parsed']['extensions']['subjectKeyIdentifier']) &&
isset($candidate['extensions']['authorityKeyIdentifier']) &&
$certificate['parsed']['extensions']['subjectKeyIdentifier'] === trim(str_replace('keyid:', '', $candidate['extensions']['authorityKeyIdentifier']))) {
$hash = getHash($certificate['pem']);
$parents[$hash] = [];
$store[$hash] = $certificate['parsed'];
}
}
}
if (count($parents) > 0) {
foreach ($parents as $hash => $arr) {
$parents[$hash] = checkParents($store[$hash], $certTypes, $rootCertificates, $intermediateCertificates, $store);
}
}
return $parents;
}
function prettyPrintChain($chain, $store, $chainNumber = 0, $chainSoFar = []) {
foreach ($chain as $key => $value) {
if (count($value) > 0) {
$history = $chainSoFar;
$history[] = $key;
prettyPrintChain($value, $store, $chainNumber, $history);
} else {
foreach ($chainSoFar as $parent) {
echo $chainNumber . ": " . $parent . "\r\n";
echo $store[$parent]['subject']['commonName'] . "\r\n";
}
echo $chainNumber . ": " . $key . "\r\n";
echo $store[$key]['subject']['commonName'] . "\r\n";
}
$chainNumber++;
}
}The script loads up the root and intermediate bundle files to work with, reads in the provided leaf certificate as a PEM encoded file and then outputs all of the possible chains it could find. The magic happens in checkParents() and what that does it check a couple of fields to help us out.
We have the subjectKeyIdentifier which is a unique ID assigned to identify the public key of the subject, or the 'owner', of this certificate/key and we have the authorityKeyIdentifier which is a unique ID assigned to identify the key that signed this certificate. Take the following basic example certificate chain:
CN:scotthelme.co.uk
SKID:12345
AKID:ABCDE
CN:Let's Encrypt X3
SKID:ABCDE
AKID:ZXCVB
CN:ISRG Root X1
SKID:ZXCVB
AKID:ZXCVBYou can see that the leaf, intermediate and root all have their own unique ID and we can follow the AKID all the way back to the root which is of course self signed. By following the AKID like this, and checking all known intermediate and root certificates for a match, we can find alternate chains. Take this example of an alternate trust path for the same leaf certificate:
CN:scotthelme.co.uk
SKID:12345
AKID:ABCDE
CN:Let's Encrypt X3
SKID:ABCDE
AKID:ASDFG
CN:DST Root CA X3
SKID:ASDFG
AKID:ASDFGWe know from my previous articles that there are two versions of the Let's Encrypt X3 Intermediate certificate and that one is signed by the ISRG Root and one is signed by the IdenTrust Root. We also know that they both contain the same Public Key as we previously discussed, which you can see as both of these intermediates have the same SKID despite being different certificates issued by different Root CAs. Let's run this against a real example and see what happens.
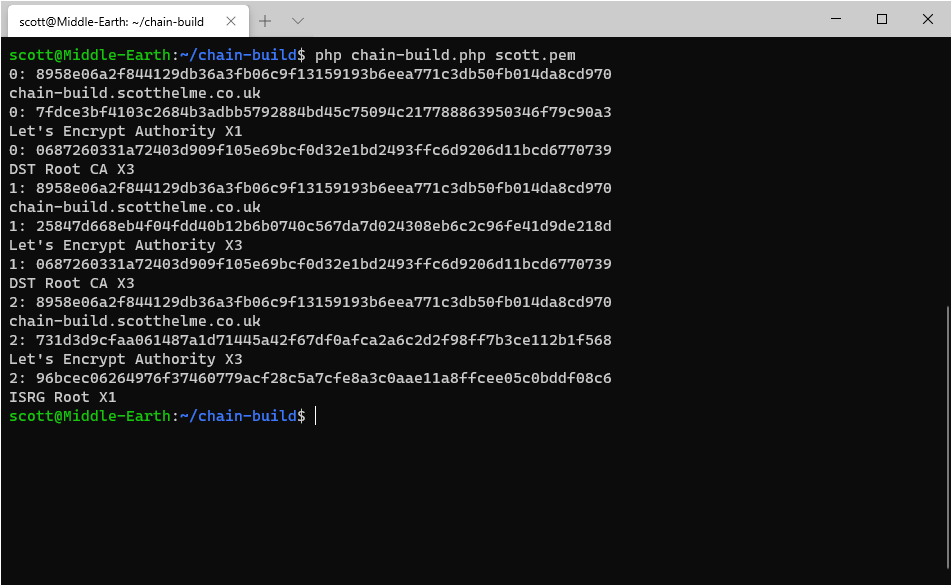
It takes only a few seconds to run and comes out with a total of 3 possible trust paths that exist for my leaf certificate. And yes, I did create another brand new certificate just to demo this! (Thanks for being awesome, easy and free Let's Encrypt!)
The output here shows the leaf certificate, all intermediates and then the root for each chain that was built. Analysing the 3 chains we have:
0: 8958e06a2f844129db36a3fb06c9f13159193b6eea771c3db50fb014da8cd970
chain-build.scotthelme.co.uk
0: 7fdce3bf4103c2684b3adbb5792884bd45c75094c217788863950346f79c90a3
Let's Encrypt Authority X1
0: 0687260331a72403d909f105e69bcf0d32e1bd2493ffc6d9206d11bcd6770739
DST Root CA X3
1: 8958e06a2f844129db36a3fb06c9f13159193b6eea771c3db50fb014da8cd970
chain-build.scotthelme.co.uk
1: 25847d668eb4f04fdd40b12b6b0740c567da7d024308eb6c2c96fe41d9de218d
Let's Encrypt Authority X3
1: 0687260331a72403d909f105e69bcf0d32e1bd2493ffc6d9206d11bcd6770739
DST Root CA X3
2: 8958e06a2f844129db36a3fb06c9f13159193b6eea771c3db50fb014da8cd970
chain-build.scotthelme.co.uk
2: 731d3d9cfaa061487a1d71445a42f67df0afca2a6c2d2f98ff7b3ce112b1f568
Let's Encrypt Authority X3
2: 96bcec06264976f37460779acf28c5a7cfe8a3c0aae11a8ffcee05c0bddf08c6
ISRG Root X1The long values there are the sha256 fingerprints of the certificates and you can easily look them up in any tool like crt.sh or Censys. Here are the links for the Let's Encrypt Authority X1 intermediate in the first chain:
https://censys.io/certificates/7fdce3bf4103c2684b3adbb5792884bd45c75094c217788863950346f79c90a3
https://crt.sh/?q=7fdce3bf4103c2684b3adbb5792884bd45c75094c217788863950346f79c90a3
Using the tool we can now look at chains for other certificates and I did an awful lot of manual analysis of the BBC certificate chain in my previous blog posts so let's have a look and see what Chain Build comes up with.
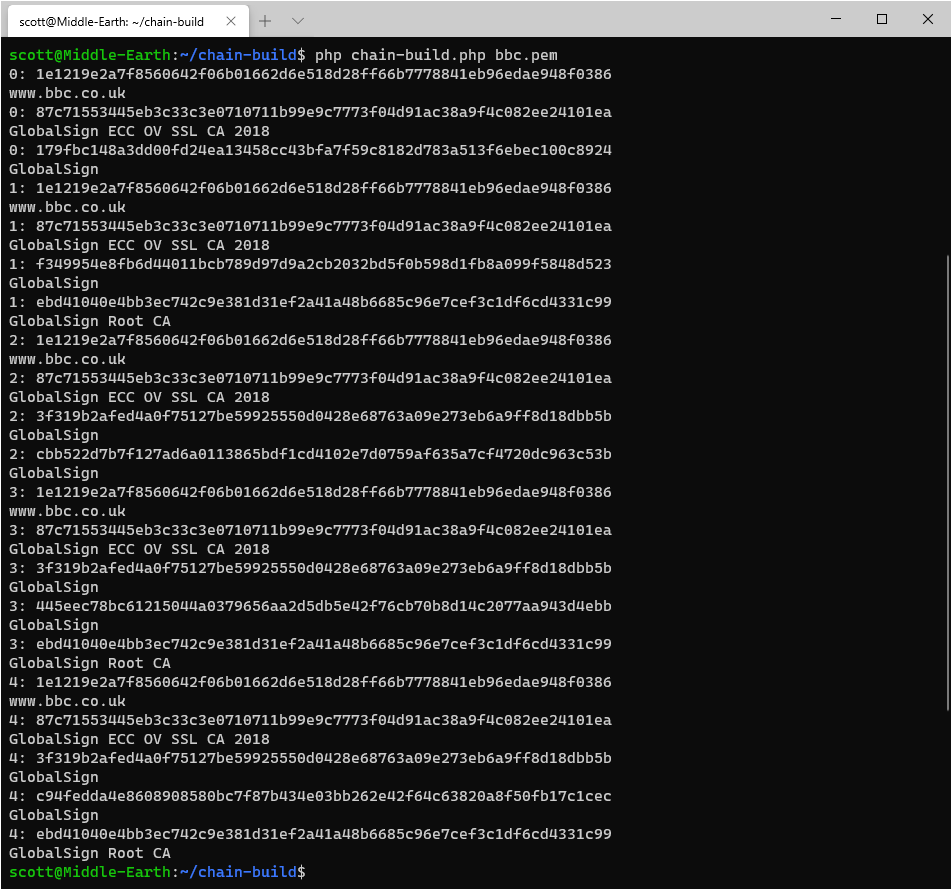
5 different chains! Good to see that we match up and I'm a little sad that Chain Build managed to do in a few seconds what it took me... a lot longer... to do manually.
You shouldn't use this tool for anything
As I said at the beginning, I created this just to show that alternate trust paths exist and that it can be quite easy to get started in identifying them. If you were going to write something to do actual chain building though, it'd need to be 100x more complex than what I've written here which doesn't even begin to scratch the surface of what's required. If you were going to depend on this to identify legacy client concerns you'd need to look at the expiration of all certificates in any of the chains identified above and you'd need to use older version of the intermediate and root stores than the ones I used. I don't want to drone on too much but this is a hacky script I wrote whilst drinking a beer to scratch an itch! Use it for education purposes but understand the severe limitations.
Lifting the fog
Hopefully this post and the above tool, along with my previous posts, have helped to clarify a few key points about certificates, certificate chains and how they work. All of the things I've covered in these recent articles, including many of the diagrams, are taken directly out of the advanced training course I run on TLS and PKI. If this stuff interests you and you want to spend 2 days on this with the ability to get hands on building it and ask me questions along the way, consider joining us! For now though, I hope you at least enjoyed this short series 👍
